История измерений формы и размеров Земли
Не все знают, что о форме и размерах Земли люди имели достаточно реальные представления еще до начала нашей эры. Так, древнегреческий философ Аристотель (384 — 322 до н. э.) полагал, что Земля имеет шарообразную форму, а в качестве доказательства приводил округлость формы земной тени во время лунных затмений, поскольку только шар при освещении с любой стороны всегда дает круглую тень.
Эратосфен, живший в Александрии (город на севере Египта, основан Александром Македонским в
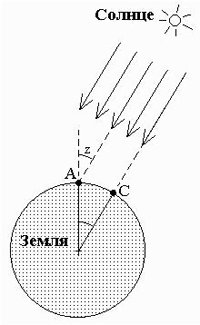 Рис. 1 |
По новейшим определениям разность широт Александрии и Ассуана равна 7°7’, и оба города не лежат на одном меридиане, (Ассуан почти на 3° восточнее Александрии), там не менее астрономическая часть работы Эратосфена для своего времени была почти безупречна. К несчастью истинная длина египетской стадии была не известна. Разные ученые исследователи определяют ее от 158 до 185 метров, и потому о точности этого первого градусного измерения в настоящее время нельзя составить себе верного представления. Во всяком случае, как упомянуто выше, основание способа Эратосфена совершенно верно и применяется до сих пор.
В связи с этим непонятно, как полтора тысячелетия (!) спустя Христофор Колумб настолько ошибся с оценкой размеров Земли, что принял Американский континент за часть Индии!
Следующая попытка определить размеры Земли была сделана Посидонием (Посидоний из Апамеи в Сирии, философ–стоик, математик и астроном,
Замечательно, что в сочинениях Птоломея (87 — 165), известного александрийского астронома, не упоминается об определении размеров Земли, хотя в его «Географии» видимо подразумевается ее шарообразность и длина одного градуса принимается равною 500 стадиям (80 км), что дает для окружности всей Земли 180 000 стадий (28 800 км) — число значительно меньшее, чем результаты Эратосфена и Посидония.
После уничтожения александрийской библиотеки, в смутные годы первых веков нашей эры, всякие научные работы прервались, и новая попытка градусного измерения сделана лишь в 827 году арабами, которые, достигнув политического могущества, в лице своих калифов с любовью покровительствовали развитию точных наук. Калиф Альмамум, сын Гарун–
Покуда длина арабского локтя была неизвестна, нельзя было составить себе понятие о точности измерения арабов; известно было лишь, что арабский локоть имел 27 дюймов, а каждый дюйм равнялся шести положенным в ряд ячменным зернам. Но недавно, на нильском острове Рода, под Каиром, на колонне из тесанного камня, найдены черты, означающие арабские локти, подразделенные на дюймы. Оказалось, что арабский локоть равен приблизительно 49⅓ сантиметрам, так что длина арабской мили выходит около 1973 метров или 926.3 саженей. От перемножения этого числа на 56⅔ получается для длины градуса, под широтой 35°, 104.8 версты (111.088 км), что весьма близко к современным определениям.
В средние века сведенья греков и арабов о шарообразности Земли и ее величине были забыты, и только в начале XVI века, после эпохи великих морских путешествий, произведена новая попытка определения размеров Земли. Именно, французский ученый и врач короля Франциска
Итак, в первом приближении форма и размеры нашей планеты известны очень давно. А можно ли, находясь на ее поверхности, доказать, что она вращается? Оказывается, можно, и даже несколькими способами.
Вращение Земли
В 1672 году француз Рише случайно заметил, что у экватора маятниковые часы идут медленнее, чем в Париже. Объяснение этому факту нашел английский физик, астроном и математик Исаак Ньютон (1643 — 1727). Вращение Земли должно приводить к появлению центробежной силы, направленной перпендикулярно оси вращения (не поверхности!) в сторону, противоположную этой оси. То есть в средних широтах центробежная сила меньше по величине (поскольку расстояние до оси вращения меньше) и направлена под углом к горизонту, а на экваторе она достигает наибольшей величины, что и приводит к уменьшению силы тяжести g на экваторе и, вследствии этого, замедлению (увеличению периода Т) колебаний маятника длиной l, поскольку T = 2p(l/g)1/2.
В 1851 году французский физик Жан Фуко (1819 — 1868) продемонстрировал на опыте, что плоскость качания маятника со временем поворачивается, что объясняется суточным вращением Земли вокруг своей оси. Позже этот опыт повторяли в разных городах, в том числе и в Ленинграде, в Исаакиевском соборе. Очевидно, что эффект поворота плоскости качания маятника зависит от широты места проведения опыта, наиболее выражен на земных полюсах и отсутствует на экваторе. Тот же Жан Фуко изобрел гироскоп, и его свойство сохранять направление оси вращения также доказывало суточное вращение Земли (ось гироскопа при любом положении за сутки опишет окружность вокруг проекции на небо земной оси, а почему — будет объяснено в главе про экваториальную систему координат).
Другим свидетельством земного вращения является действие поворотного, или кориолисова ускорения на движущиеся воздушные и водные массы. Этот эффект проявляется как отклонение от меридианального направления ветров и океанских течений, а также в подмывании одного из берегов реками, текущими в направлении север — юг. Суть явления очень проста. Если, например, река течет с юга на север, то ее воды по инерции стремятся сохранить ту линейную скорость вращения (перпендикулярную направлению течения), которую они имели южнее, т. е. отклониться к востоку (Земля вращается с запада на восток). А в результате будет размываться восточный берег.
И еще одно доказательство вращения Земли — отклонение падающих тела от направления отвесной линии. Объяснение точно такое же: линейная скорость вращения тем больше, чем выше над поверхностью тело, а при падении эта скорость сохраняется, и за время полета точка, прямо над которой сначала находилось падающее тело, сместится на восток на меньшее расстояние, чем само тело в момент приземления, т. е. тело упадет восточнее.
Более точная форма Земли
Зная период вращения (24 часа) и радиус Земли легко вычислить линейную скорость вращения на экваторе: v0 = w R, где w = 2p/86400 об/сек, и при R = 6378 км получается v0 ~ 460 м/c (на широте j эта скорость составит v = v0*cos(j)). На тело массой m будет действовать центробежная сила Fц = m*w2*R и сила тяжести по закону всемирного тяготения Fg= G*M*m/R2, где М — масса Земли, R — ее радиус. Отношение Fц к Fg для шарообразной Земли составит:
Fц / Fg= w2*R3/(G*M) (2)
Если подставить сюда реальные значения М и R, то получим Fц / Fg= 3.45×
Теперь самое время вспомнить, что форма Земли
Такой расчет не так уж и сложен. Нужно прировнять вес каждого элементарного объема вещества на полюсе и на экваторе. То есть для равновесия на любом расстоянии r от центра Земли будет справедливо соотношение:
m*gп(r)=m*gэ(r) — m*w2*r (3)
Зависимость ускорения свободного падения от радиуса в полярном и экваториальном колодцах одинакова: gп(r) = gэ(r) = GM/r2, где М — масса, заключенная внутри радиуса r : M(r) = r*4*p*r3/3, где r — плотность вещества, заполняющего колодцы. Если все это подставить в уравнение равновесия (3), сократить на m и проинтегрировать по всему радису Земли (левую часть — от 0 до полярного радиуса Rп, правую — от 0 до экваториального радиуса Rэ), то в результате получится соотношение:
Rп = Rэ*(
Подставив в (4) среднюю плотность Земли 5.52 г/см3 (она
Таким образом, еще Ньютон показал, что Земля должна быть сплюснута у полюсов. То же самое следовало и из наблюдений быстровращающихся планет–гигантов — Юпитера и Сатурна. Однако проверить это на практике в отношении Земли было совсем не просто. Только в следующем веке было организовано несколько экспедиций специально для того, чтобы измерить длины двух дуг меридиана, по 1° каждая, одна как можно ближе к экватору, другая — к полюсу. В конце концов выяснилось, что дуга в 1° в экваториальных широтах (измерения 1735 — 1743 гг. в Перу) действительно короче, чем в полярных (
Кстати, результатом этих экспедиций стало также принятие новой единицы длины, которую определили как 1/40 000 000 часть от полной длины Парижского меридиана. Эта единица получила название метр, и поэтому неудивительно, что длина земного экватора так близка к круглому числу 40 000 км. Принятие новой единицы длины стало началом введения метрической системы мер и весов, а сам метр был выполнен в виде массивного стержня из сплава платины с иридием, переданного на вечное хранение в парижский архив. Последующие исследования показали, что принятая длина метра немного занижена по отношению к сорокамиллионной доли от окружности Земли, но менять стандарт сочли неразумным, так как каждое новое измерение вносило бы новые поправки, да и разные меридианы несколько отличаются по длине, так как фигура Земли не совпадает с эллипсоидом вращения. В настоящее время величина метра закреплена более точно и надежно, а до
Раз уж речь зашла о единицах длины, то стоит рассказать еще об одной. Поскольку полная длина меридиана принята за 40 000 км, то 1° от этой длины составит в среднем 1/360 его часть, что равно 111.111 км, а 1’ — 1.852 км. Последняя единица называется морской милей. Ее удобство для навигации, особенно в прошлые века, определяется тем, что широту местности вычисляют по высоте светил (например, Солнца в момент его наибольшей высоты) над горизонтом, а изменение высоты светила на 1’ (за счет движения на север или на юг) как раз и соответствует перемещению наблюдателя на 1 морскую милю вдоль меридиана.
Осталось только упомянуть, что при еще более точном рассмотрении форма Земли отличается от эллипсоида вращения, и в масштабах меньше километра имеет весьма сложную форму поверхности, которая получила названия геоида. Между прочим, под поверхностью Земли в данном случае подразумевается не реальный рельеф поверхности со всеми горами, холмами и низинами, а усредненный уровень воды в океанах, который с помощью нивелирования удается продолжить и под сушей (высота над уровнем моря). Эта поверхность является уровневой, т. е. она всюду перпендикулярна к направлению силы тяжести и отличается от эллипсоида вращения не больше, чем на несколько сотен метров, а если за фигуру Земли принять трехосный эллипсоид (экватор можно представить как эллипс с разностью полуосей около 200 м), то отличие геоида от него не превысит 100 м. Это отличие вызвано неравномерным распределением масс как на поверхности Земли (континенты и океаны), так и внутри нее — вследствии их влияния на величину и направление силы тяжести. Изучение фигуры геоида — одна из задач геодезии и гравиметрии.
Масса Земли
Массу Земли с достаточной точностью измерил в 1797 году Генри Кавендиш. Для этого он использовал крутильные весы со свинцовыми шариками на концах. Приближая к этим шарикам с разных сторон два больших свинцовых шара и зная их массы, по углу закрутки весов Кавендиш измерил, во сколько раз сила притяжение маленького шара к большому отличается от силы притяжения Земли. В итоге масса Земли получилась 6×1021 тонн, что близко к значению, принятому в настоящее время.
Теперь снова вспомним закон всемирного тяготения. Ускорение, сообщаемое тяготение Земли любому телу на ее поверхности, называется ускорением силы тяжести. Оно направлено примерно к центру Земли и по величине приближенно равна:
g = G*M/r2 (5)
где G — гравитационная постоянная, M — масса Земли, r — ее радиус. Если бы Земля не вращалась и имела форму шара со сферически–симметричным распределением масс внутри себя, то выражение (5) было бы точным. Однако на самом деле эти три условия не выполняются.
Направление силы тяжести для эллипсоидальной формы Земли немного отличается от направления на геометрический центр эллипсоида, совпадая с ним на экваторе и полюсах, и достигая максимальной величины отклонения (5’.7) на широтах +–45°. В то же время на экваторе величина силы притяжения
Кроме того, в ускорение силы тяжести входит центробежное ускорение, возникающее от суточного вращения Земли. Оно направлено перпендикулярно оси вращения, по радиусу r образованного параллелью круга и лежит в его плоскости. Центробежное ускорение равно w2*r, где w = 2*p/Т — угловая скорость вращения с периодом Т, причем для Земли нужно взять продолжительность звездных суток Т = 86146 с. На экваторе центробежное ускорение максимально: w2*r = 3.39 см/с2, что составляет 1/288 долю от гравитационного ускорения силы тяжести, равного на экваторе 983.42 см/с2. На экваторе центробежная сила прямо противоположна силе притяжения и поэтому вычитается из последней, что дает полное ускорение свободного падения g = 980.03 см/с2. На полюсах центробежная сила отсутствует и не дает боковой составляющей.
В промежуточных широтах центробежная сила пропорциональна радиусу параллели r = r*cos(ja), где r — текущее расстояние до центра Земли (радиус–вектор), а ja — геоцентрическая широта. Отличие ja от обычной географической широты j составляет j — ja = 11’.6*sin(2*j). Поэтому центробежное ускорение w2*r = w2*r*cos(ja) можно разложить на вертикальную составляющую w2*r*cos(ja)*cos(j) и горизонтальную w2*r*cos(ja)*sin(j), направленную по меридиану к экватору. Если пренебречь небольшим различием между ja и j, то горизонтальная составляющая центробежного ускорения w2*r*cos(j)*sin(j) будет максимальной на широте +–45°, достигая значения 1.7 см/с2, что в угловой мере соответствует отклонению отвеса на 5.’9 к югу. Вертикальная составляющая центробежного ускорения w2*r*cos(j) (если пренебречь различием между направлением отвесной линии и направлением на центр Земли) на экваторе даст w2*r, на широтах +–45° — 0.5*w2*r и нуль — на полюсах. Таким образом, на экваторе ускорение силы тяжести уменьшено на f за счет центробежной силы и на f/2 за счет уменьшения силы притяжения. В сумме эти два эффекта приводят к тому, что на экваторе ускорение силы тяжести на f/2+f = 1.5*f ~ 1/200 меньше, чем на полюсах.
Точную зависимость ускорения силы тяжести от высоты вывел в 1743 г. французский математик А. Клеро:
g = g0*(1+b*sin2(j)), b = (g0 — gp)/g0 (6)
где g0 — ускорение силы тяжести на экваторе, gp — на полюсе, а коэффициент b = 2.5*q — f (здесь q — отношение центробежного ускорения к ускорению силы тяжести на экваторе w2*r/g0 , f — сжатие Земли). В современных числовых значениях формула Клеро выглядит так:
g = 978.03*(1+0.00529*sin2(j)) (7)
Измерение ускорения силю тяжести в разных местах позволяет определить числовое значение b, а через него — сжатие Земли f, которое оказалось в хорошем согласии с измерениями дуг меридианов. Ускорение силы тяжести можно измерить несколькими способами, из них самый простой — по периоду качания маятника известной длины l:
T = 2*p*(l/g)1/2, откуда g = 4*p2*l/T2 (8)
Измерением и изучением распределения ускорения силы тяжести по поверхности Земли занимается специальный раздел астрономии — гравиметрия. Это распределение позволяет не только получить величину сжатия Земли, но и найти отклонения фигуры геоида от точного эллипсоида и, кроме того, получить важные сведения о внутреннем строении Земли.
Из величины ускорения силы тяжести легко получить массу и среднюю плотность Земли. Например, на широте 45° по формуле Клеро (7) g = 980.62 см/с2. Вертикальная составляющая центробежного ускорения на этой широте составит 0.5*w2*r = 1.7 см/с2. Отсюда ускорение силы притяжения на широте 45° получится 982.32 см/с2. Подставив эту величину и средний радиус Земли r = 6.370×108 см в фомулу Ньютона (5), получим массу Земли М = 5.98×1027 г. Среднюю плотность Земли можно вычислить, если разделить массу М на объем Земли, что даст 5.52 г/см3.
Параметры Земли
- Экваториальный радиус а = 6378.140 км
- Полярный радиус b = 6356.755 км
- Средний радиус r = 6371.004 км
- Радиус–вектор на уровне моря на широте j: r = a*(0.998 324 07 + 0.001 676 44*cos(2*j) — 0.000 003 52*cos(4*j) + …)
- Сжатие Земли fe = (
a–b )/a = 0.003 352 81 = 1/298.257 - Эксцентриситет земного меридиана e = ((
a2–b2 )/a2)1/2 = 0.081 820 - Площадь поверхности 509 494 365 км2,
- из них суша — 29.2%,
- водная поверхность — 70.8%
- Объем Земли 1.083 209×1012 км3
- Масса Земли 5.973×1027 г = 1/(332 946 +– 20) массы Солнца
- Средняя плотность Земли 5.574 г/cм3
- Средняя плотность земной коры 2.80 г/cм3
- II космическая скорость у поверхности 11.2 км/с
- Длина 1o географической долготы на широте j (111.321*cos(j) — 0.094*cos(3*j)) км
- Длина 1o географической широты на широте j (111.143 — 0.562*cos(2*j)) км
- Разность астрономической j и геоцентрической j’ широт (в системе МАС) j — j’ = 692«.74*sin(2*j) — 1».163*sin(4*j) + 0«.003*sin(6*j)
- Угловая скорость вращения Земли 15».041/с = 0.000 072 921 об/с
- Линейная скорость точки земной поверхности на широте j: v = 465.119*cos(j) м/с
- Средняя скорость орбитального движения Земли 29.765 км/с ~ 100 000 км/ч
- Наибольшая орбитальная скорость (в перигелии) 30.287 км/с
- Наименьшая орбитальная скорость (в афелии) 29.291 км/с
- Год звездный (период обращения вокруг Солнца относительно звезд) 365.25636 суток = 365 д 6 ч 9 мин 10 с
- Год тропический (период обращения вокруг Солнца относительно точки весеннего равноденствия) 365.24220 суток = 365 д 5 ч 48 мин 46 с
- Год аномалистический (период обращения вокруг Солнца относительно перигелия) 356.25964 суток = 365 д 6 ч 13 мин 53 с
- Год драконический (период обращения вокруг Солнца относительно узлов лунной орбиты) 346.62003 суток = 346 д 14 ч 52 мин 51 с
- Ускорение Земли к Солнцу 0.59 см/с2
- Ускорение силы тяжести на поверхности Земли (стандартное) g0 = 980.665 см/с2
- Ускорение силы тяжести на широте 45o (абсолютное) g45 = 980.616 см/с2
- Ночное излучение Земли (в ясную ночь)
70—140 Дж/м2/с