Главная » ГеоИстория » Интересные сведения

Понятие о градусном измерении

Попытки определить размеры земного шара принадлежат ко временам глубокой древности: еще халдеи полагали, что всю Землю можно обойти за один год. Но первые научные указания на вид и размеры Земли находятся в сочинениях Аристотеля (384—322 до Р. X.); именно в трактате «О небе», в книге II–ой, этот философ приводит доказательства шарообразности Земли и прибавляет, что, по мнению современных ему математиков, окружность земного шара равна 400 000 стадиям или 64 000 км; (Стадия — мера длины, равная 160 м) но каким образом было получено это число, Аристотель не объясняет. Поэтому истинным основателем Геодезии, как науки, признается Эратосфен (276—196 до Р. X.), ученый, заведовавший знаменитой александрийской библиотекой в царствование Птоломея III–го. Он вывел размеры Земли по способу, в общих чертах применяемому и в настоящее время, именно при помощи так называемого градусного измерения.

Черт. 1

Черт. 2

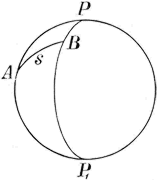
Пусть на шарообразной поверхности Земли определены широты и долготы двух точек А и В (черт. 1) и измерено линейное расстояние между этими точками. Из решения сферического треугольника АВР, образованного меридианами точек А и В и дугой большого круга АВ, по данным двум сторонам АР и ВР (в предположении, что Земля шарообразна, дуги меридианов АР и ВР будут дополнениями широт точек А и В до 90°) и углу между ними АРВ (представляющему разность долготе этих же точек) легко вычислить угловую величину дуги АВ, т. е. сколько в ней градусов, минут и секунд; пусть она содержит σ״. Зная с другой стороны, линейную длину той же дуги АВ = s и называя радиус земного шара через R, можно составить пропорцию:

откуда

где

Из этой формулы радиус получается конечно в тех же линейных единицах, в которых выражена длина дуги s. 

Точность вычисления радиуса R зависит от точности, с которой известны входящая в формулу (1) числа s и σ; первое получается измерением линейного расстояния между точками А и В, а второе — из решения сферического треугольника АРВ, так что точность определения σ зависит от точности, с которой известны широты и долготы точек А и В. Так как широты определяются точнее, чем долготы, то самый выгодный случай для вывода углового расстояния σ есть тот, когда обе точки А и В лежат на одном меридиане. Легко понять, что в этом случае решение сферического треугольника устраняется и определение σ сводится к изысканию разности широт точек А и В; эта разность широт может быть получена простейшим способом из одновременного измерения высот какого–нибудь светила (Солнца или звезды) в точках А и В, когда светило находится в плоскости общего их меридиана.

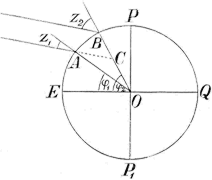
Пусть высоты светила в точках А и В (черт. 2) будут h₁ и h₂, зенитные расстояния его z₁ и z₂, причем

и 

а широты этих точек соответственно и (EQ — экватор).

Угол σ равен углу AOB между радиусами АО и ВО. Продолжив направление на светило в А до встречи с ВО в точке С и замечая, что, по отдаленности светила от Земли, направления на него из А и В можно считать параллельными, имеем:

или

но из чертежа видно еще, что

поэтому

т. е. разность высот светила, одновременно измеренных на двух точках, лежащих на одном меридиане, действительно равна разности широт этих точек. Зная линейное расстояние s тех же точек, не трудно вычислить длину одного градуса, которую назовем через D, из пропорции

откуда

Итак, определение разности широт двух точек на одном меридиане в связи с измерениями их линейного расстояния позволяет вычислить длину одного градуса; вот почему подобная работа называется градусным измерением. Зная длину одного градуса, не трудно вычислить длину всей окружности и ее радиус. Каждое градусное измерение состоит из двух отдельных действий: определения угла, составленного отвесными линиями двух точек, и определения линейного расстояния между ними; первое составляет астрономическую, а второе — геодезическую часть градусного измерения.

Из предыдущего легко видеть, что всего проще произвести градусное измерение по меридиану, но оно может быть выполнено и по параллели, или вообще в любом направлении. Геодезические действия остаются во всех случаях одинаковыми, и разница заключается лишь в действиях астрономических. Для градусного измерения по меридиану надо определить только разность широт конечных точек, а для измерения по параллели или в произвольном направлении необходимо определить еще разность долгот.